Muy bueno Fabio, Muchas gracias.
Es imposible medir la longitud de la costa de un país, tiende a infinito (!)

Lo que dice el título es cierto, no hay forma de medir la distancia de la costa de un país y, cuanta más precisión le ponemos al asunto, más tiende al infinito.
No estoy loco, es un problema fractal, porque, al fin y al cabo ¿Qué es una costa? ¿Cómo se mide? Cada país tiene su propia forma de medir el litoral marítimo y este problema se da, usualmente, en las costas ya que las fronteras arbitrarias hechas en un mapa son fáciles de medir, tienen líneas rectas y se logran mediante acuerdos. Pero ¿el mar? Ah, es otro tema.
Hoy hablamos de una nerdada llamada la "Paradoja de la línea de costa".
No hay un estándar de "resolución" para medir una distancia, cada país decide si usará un metro, una decena, una centena, esto hace imposible tener precisión ¿Cuánta sería la correcta? Obviamente podemos definir un metro como algo más útil pero a nivel de kilómetros tal vez sea demasiada precisión que nadie necesita.
El problema se va dando en la medida que "hacemos zoom" sobre una costa que suele ser irregular, si tmmos un metro de resolución nos puede dar una costa de 400 kilómetros en total, si pasamos a 10 centímetros podemos llegar a 5000km y si miramos centímetro a centímetro, al sumar todo, estaremos por los 50.000km o más, no sabemos, porque ESE es el problema.
Por ende, como no hay un estándar, cada país mide las costas como se le canta.
Un ejemplo visual para que se entienda:
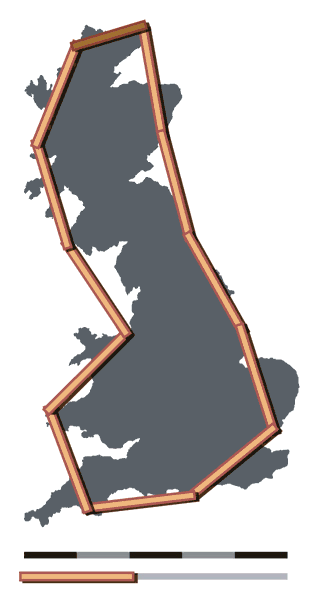
Si medimos la costa de Gran Bretaña utilizando rectas de 200km nos dará una costa total de 2400km.
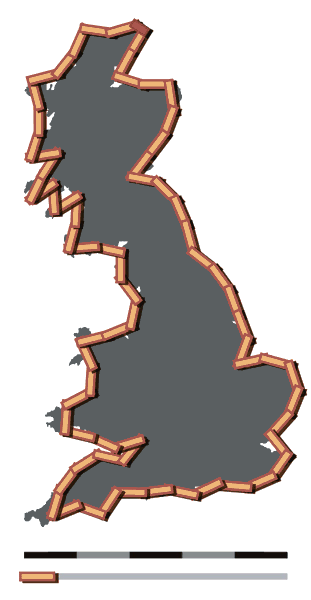
Si cambiamos a una resolución de 50km la costa ahora nos mide 3400 kilómetros.
En un verdadero fractal la longitud diverge hacia el infinito, en el caso de las costas no es tan así pero se aproxima en complejidad a los fractales. Las costas no son fractales pero se comportan como tales.
Pero yendo a la realidad, por ejemplo, utilizar una resolución de un centímetro no tiene ningún sentido práctico a la hora de medir las costas de un país, con una medida mucho mayor es más fácil para cualquier gobierno.
Pero ahí yace el problema: no existe un estándar.
Cómo se dieron cuenta
En 1951 Lewis Fry Richardson estaba investigando sobre el efecto en la distancia de fronteras y la probabilidad de guerra, uno de esos papers que nadie leería jamás.
Se dio cuenta que Portugal reportaba una frontera con España de 987 kilómetros mientras que para los españoles era de 1214Km.
Aquí es donde comenzó el problema de las costas, ya que cada país medía como se le ocurría, ninguno de los dos estaba mal, sólo que no iban a coincidir nunca.
Ahora se lo llama el "Efecto Richardson": la suma de los segmentos aumenta monótonamente cuando la longitud común de los segmentos disminuye. En efecto, cuanto más corta sea la regla, más largo será el borde medido; los geógrafos españoles y portugueses simplemente usaban reglas de diferentes longitudes.
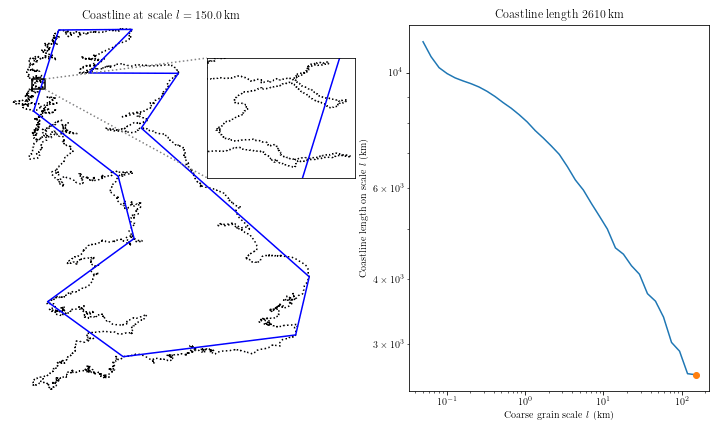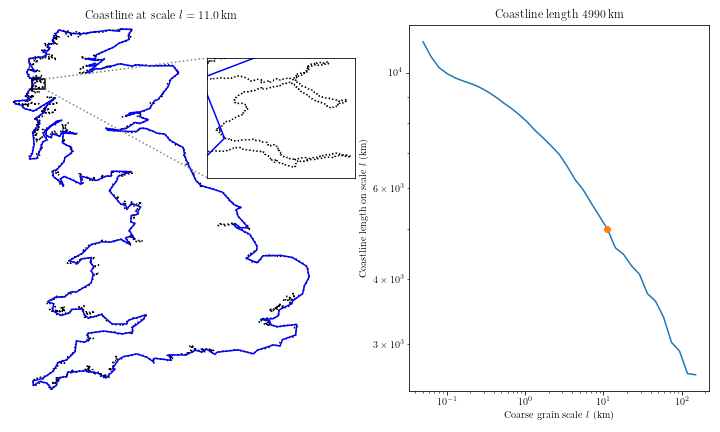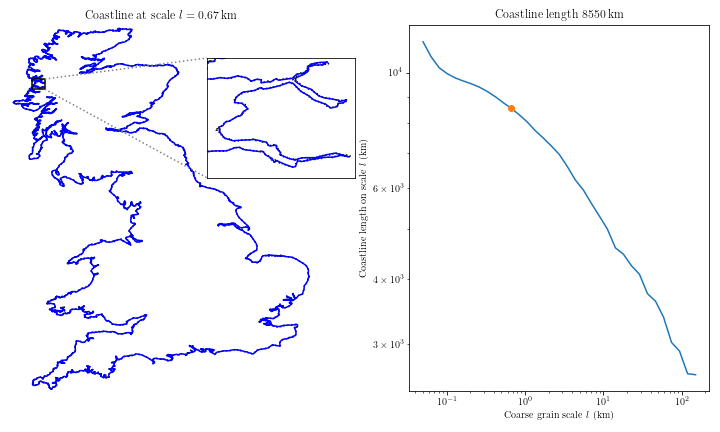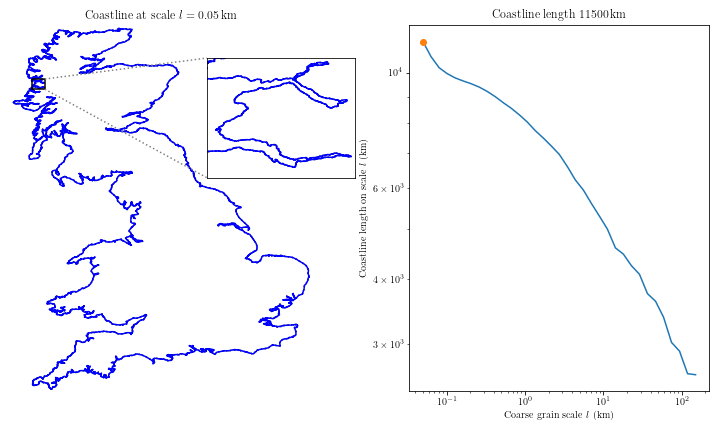
Hay más aspectos matemáticos que no son para todos, les dejo el enlace a Wikipedia que lo explica bien, también se metió de lleno en el problema el más famoso de todos, Benoit Mandelbrot, quien desarrolló una nueva rama de las matemáticas, la geometría fractal, para describir complejos no rectificables en la naturaleza como la línea costera infinita. Su propia definición de la nueva figura que sirve de base para su estudio es:
"Acuñé fractal del adjetivo latino fractus. El verbo latino correspondiente frangere significa "romper": crear fragmentos irregulares. Por lo tanto, es sensato... que, además de "fragmentado"... fractus también signifique "irregular"."
En "How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension", publicado el 5 de mayo de 1967, Mandelbrot analiza las curvas autosemejantes que tienen una dimensión de Hausdorff entre 1 y 2. Estas curvas son ejemplos de fractales, aunque Mandelbrot no utiliza este término en el artículo, ya que no lo acuñó hasta 1975. El artículo es una de las primeras publicaciones de Mandelbrot sobre el tema de los fractales.
Cabe destacar que las costas sí son finitas, no son una ecuación de Mandelbrot, y a fines prácticos todo esto se puede resolver usando la misma regla en todos los países, pero, como nadie lo hace, el efecto fractal se aplica y nos deja una nota matemáticamente "divertida". 😁
La pregunta ahora es ¿Cuánto mide la costa Argentina? ¿Estará bien ese número?
Otros posts que podrían llegar a gustarte...
Comentarios
-
Es interesante. Me preguntaba ahora con la tecnología actual de medición por satélite seria una solución. Pero siempre se caerá en el mismo problema tal como decís, cuanto mas zoom, mas precisión, el numero de la longitud aumentaría exponencialmente

-
La Costa Argentina mide 6816 km usando un segmento de 1cm (Gerardo Perillo 2005)
Por otro lado, usando un segmento de 500m la armada y el ejercicio llegaron a dos medidas distintas: 4725 (IGM) y 5087 (SHN). No encontré por qué de está diferencia pero puede ser por tema de dónde se toman los vértices de los segmentos.
-
Hay un video de Un Mundo Inmenso que explica esto https://www.youtube.com/watch?v=0cq7Hsunr10
canal super recomendado