Pi es un invento de la NASA masonica. La cuadratura del circulo es un misterio perteneciente solo a dios y no a simples mortales como nosotros.....
La Cuadratura del Círculo
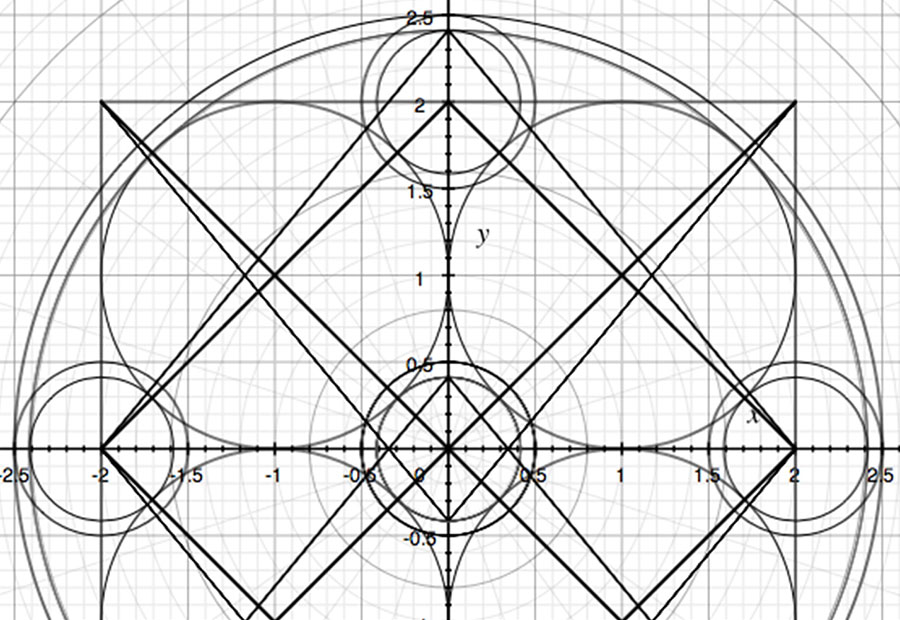
Desde la antigüedad varios se plantearon un problema matemático muy interesante, pero al mismo tiempo irresoluble. Querían hallar sólo con regla y compás un cuadrado con la misma área que un círculo dado. Lamentablemente para aquellos que gastaron siglos de tiempo y pensamiento era algo que sólo se podía resolver con repeticiones sucesivas pero no existía resolución al "problema".
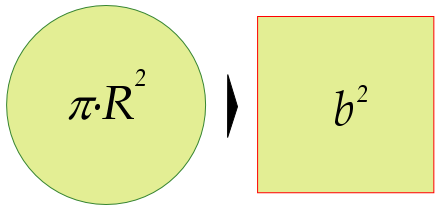
Por esta razón se sigue usando el término "cuadratura del círculo" para mencionar algo imposible de resolver o muy difícil, inconseguible.
Para el problema había que aprender primero otras cosas como el número Pi pero en 1882 el matemático alemán Ferdinand Lindemann probó que π es un número trascendente, lo que implica que es imposible cuadrar el círculo usando regla y compás, resolviendo completamente el problema. Hasta el famoso Ramanujan tuvo una aproximación genial pero la imposibilidad no le impidió a algunos querer forzar π , así es, hubo una época en la que se quizo forzar la cuadratura del círculo... por ley.
Era el año 1897 y en la asamblea general de Indiana, en los EEUU, se dio un caso genial, el de querer establecer una verdad matemática por una ley, algo absolutamente ridículo pero muy divertido viéndolo a la distancia.
Edward J. Goodwin era un matemático amateur que mediante esta ley pretendía cuadrar el círculo, así, de prepo, pero había un problema: para eso debería cambiar Pi.
No es que todos los días podamos cambiar las leyes naturales del universo, pero 3.2 no es 3.141592... etc. no importa quién lo diga, Pi te gana siempre.
De tan amateur que era Goodwin ni siquiera menciona a Pi en su texto pero sí la relación de diámetro y circunferencia, en sus cálculos, para que le cierren, debía dar 3.2 y sus justificaciones me suenan muy conocidas porque vi varias de muchos de los estafadores habituales con los que me cruzo en comentarios
"... sus soluciones de la trisección del ángulo, la duplicación del cubo y la cuadratura del círculo han sido ya aceptadas como contribuciones a la ciencia por la American Mathematical Monthly ... Y es necesario recordar que hasta no hace mucho estos problemas habían sido declarados por las academias científicas como misterios insolubles más allá de la comprensión humana."
Si, vamos, genio de Goodwin que al momento de votarse la ley el pueblo de Indiana tuvo la suerte de que otro matemático se encontraba en la sala para explicar las inconsistencias de los métodos de Goodwin que básicamente no se sostenían por ningún lado.
Si quieren leer el texto original de la propuesta está aquí.
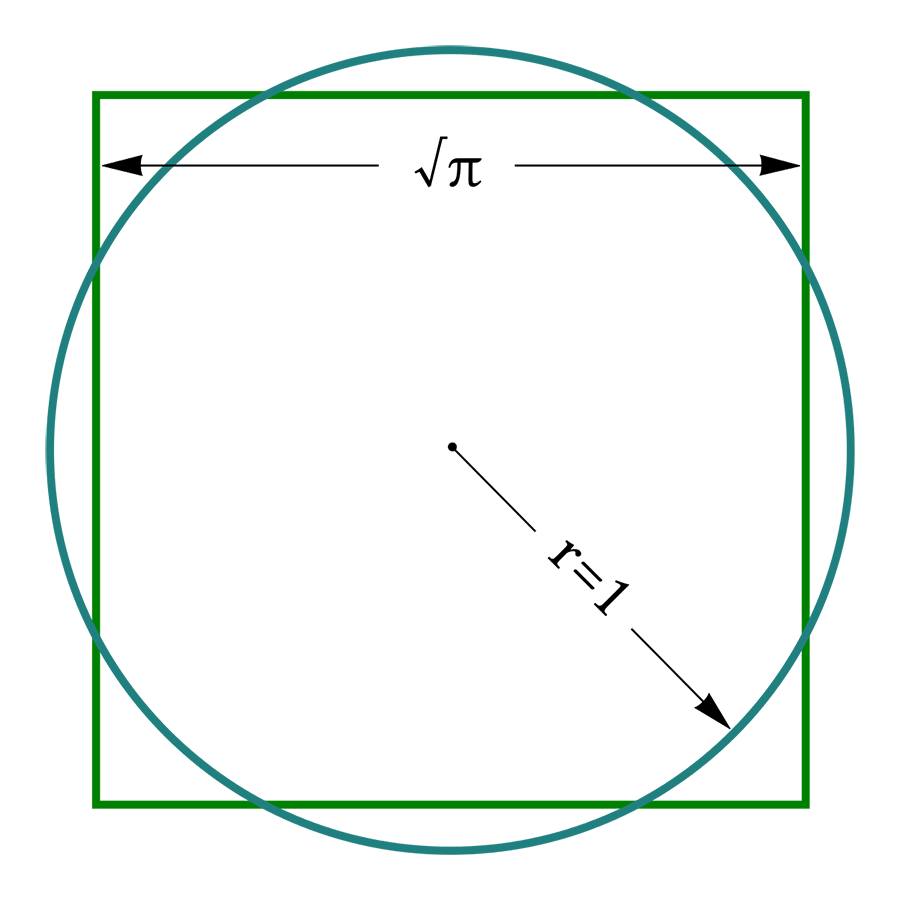
Si fuera posible cuadrar el círculo, se podría obtener raíz de π con regla y compás, es decir, se lograría obtener raíz de π por medio de operaciones algebraicas. Sin embargo, los números trascendentes son un subconjunto de los números reales que se caracterizan, entre otras cosas, precisamente por no ser obtenibles a partir de tales operaciones. Si π es un número trascendente, como demostró Lindemann, raíz de π también lo es. De aquí la imposibilidad de cuadrar el círculo a la manera griega.
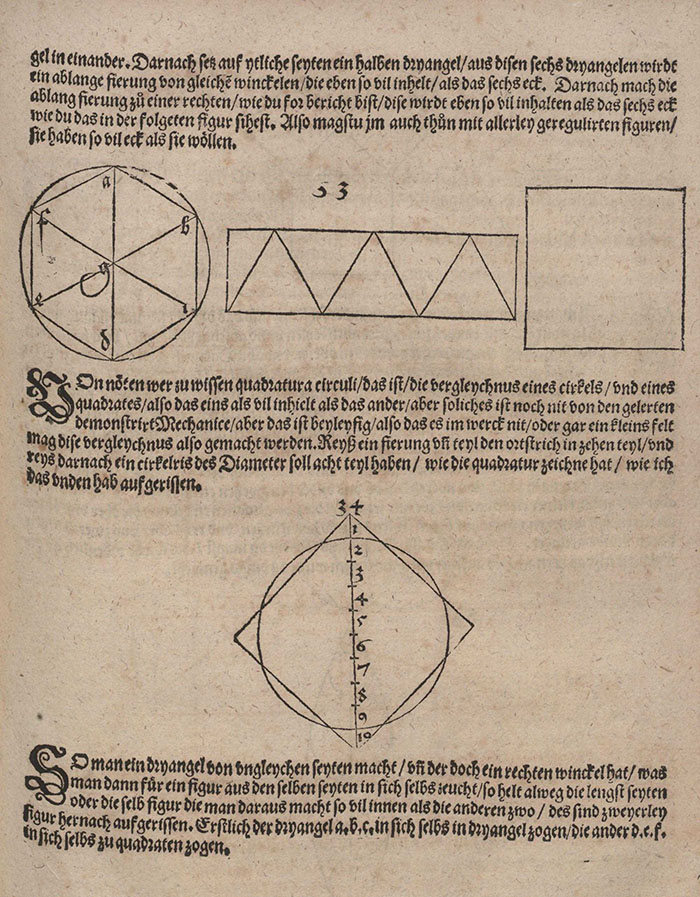
Durero también lo intentó
Ahora bien, no es que no se pueda aproximar un número, sólo que la relación con el compás y la regla es imposible, pero siempre se puede aproximar y eso hizo Ramanujan en 1914 ya que con 355/113 le daba un valor de Pi hasta los seis decimales. Nada mal!
Ramanujan
Varios matemáticos fueron dando mejores aproximaciones sabiendo que nunca daría perfecto pero ¿Quién detiene a un matemático con tiempo? Aaah, la hermosura de la matemática y el ocio creativo.
Tiempo antes Kochański tuvo esta aproximación
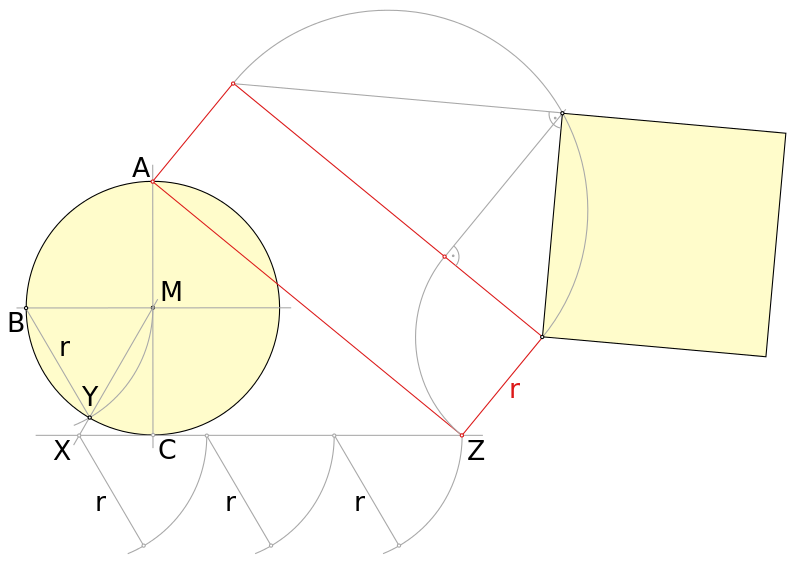
o podemos ver esta otra:
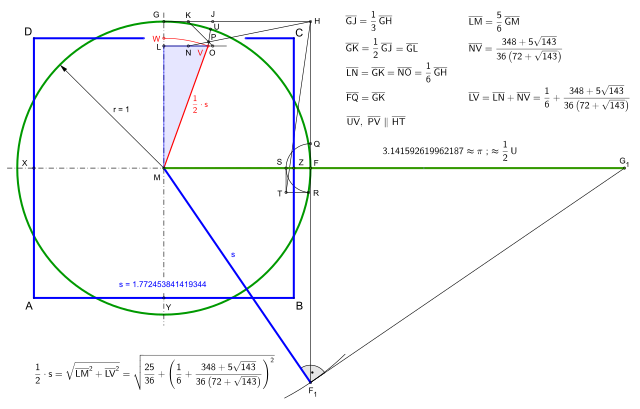
Todas estas cuadraturas fueron creadas por gente que sabía que no se podía pero querían llevar el experimento al máximo, sin embargo nunca faltará algún iluminado que proponga un nuevo método para obtener la cuadratura del círculo, lo bueno de la matemática es que cientos de mentes podrán probar si está en lo cierto o no, por lo pronto Lindemann sigue acertando y Pi se sostiene firme
Fuentes: 1, 2, 3, 4
Otros posts que podrían llegar a gustarte...
Comentarios
-
Alejandro dijo:
De esto a un post de la tierra plana no falta nada!!!

Yo creo que la ley de Goodwin explica claramente la Tierra plana, al menos en términos reptilianos. Pi = 3.2, punto, y que el multiverso se acomode o le mandamos un apercibimiento.
-
Nunca entendí la finalidad de hallar la cuadratura del círculo. Siempre me sonó a manzanización de las peras o dulcificación de la sal.

-
Hay un gran video del canal Numberphile que hace referencia a este tema, sobre todo explicando que "reglas" tenían los antiguos griegos... muy interesante!!
https://www.youtube.com/watch?v=CMP9a2J4Bqw
PD: Tiene subs en inglés y español.






