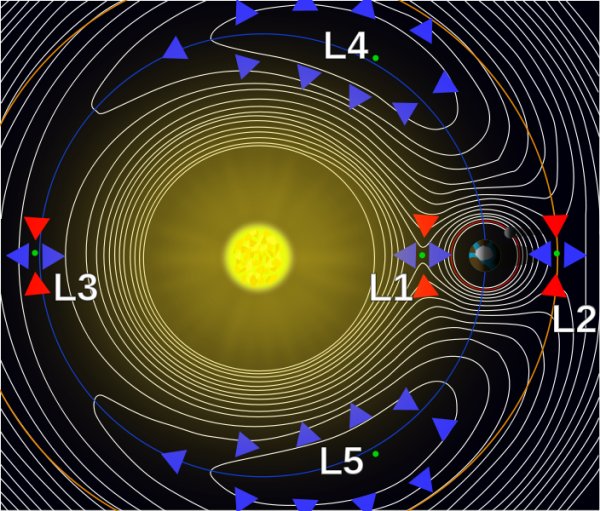
Hay unos lugares en el espacio en que más o menos está todo en equilibrio, me refiero a los puntos de Lagrange, lugares donde la gravedad no te tira ni para un lado ni el otro, la fuerza que te acerca a uno u otro planeta es la misma y te quedás, en teorÃa quieto.
El origen del descubrimiento de estos puntos viene desde hace muchos años cuando las leyes de Kepler no estaban hechas para pensar en más de dos cuerpos celestes, apenas contemplaban a dos, pero el caso ejemplo más obvio para nosotros es el sistema sol-tierra-luna, ya son tres, nos complica todo.
Vale aclarar, las órbitas, casi todas, son elÃpticas, asà que no se trata de puntos fijos, son áreas como se puede ver en el gráfico que ilustra este post. En esas cinco porciones de espacio podrÃas estacionarte con tu nave espacial sin gastar energÃa para mantener la posición, simplemente quedándote ahà mirando el planeta girar alrededor del sol y acompañarlo en ese viaje estelar.
Es un excelente lugar para poner una estación espacial, sea para estudio del espacio como para base de abastecimiento para misiones interplanetarias y esa es una de las razones por lo cual estan en boga hoy en dÃa, establecer allà una base permanente para cargar combustible o dar el salto hacia otros planetas.
El punto L1 es el más obvio para la lógica simple, si un objeto se encuentra entre la tierra y el sol en lÃnea recta el astro mayor obviamente será el que más influye pero la Tierra lo "frenará" un poco, tironea para su lado, hay una interacción entre ellos.
Ese punto obviamente está muy cerca de la Tierra porque no tiene tanto efecto gravitacional como el Sol por la diferencia de masa, lo genial de este punto es que nunca es eclipsado ni por la Tierra (que queda detrás) ni la Luna (ya que el punto está a unos 1.500.000 km de nuestro planeta (la luna a 300.000)
El punto L2 es justamente lo mismo pero del otro lado, es un lugar genial para observatorios porque la Tierra hace de escudo permanente tanto de la luz como la radiación del Sol.
Hay muchas misiones a los puntos L1 y L2 porque son los más estables, las misiones GRAIL, ACE, ISEE-3, SOHO, WIND estan allÃ, en L2 estan los observatorios Hershel, Plank, misiones como la WMAP y Chang'e 2
Y hay muchas más en planificación, algunas apuntan a los L2 entre Tierra-Luna, como la Lunar Far-Side Communication Satellites planificada en 1968 o la más moderna Exploration Gateway Platform propuesta el año pasado para justamente utilizar como un punto de reabastecimiento para misiones a la Luna, Marte y otros planetas.
Estos lugares tarde o temprano se utilizarán, lo genial de esto es encontrar formas de usar la gravedad a favor y que no sea simplemente una fueza que se te pone en contra. El caso ejemplo más conocido es el de utilizar una órbita en particular para acelerar una nave espacial, ya se ha utilizado varias veces, desde usar a Venus o la Tierra misma para tomar impulso hacia Marte o Júpiter.
Bueno, en este caso es para ubicarse quietito en un mismo lugar, asà como las órbitas geoestacionarias alrededor del planeta que sólo aplican a dos cuerpos (por eso son tan cercanas al planeta).
No nos olvidemos del uso de L3 en varias obras de ficción, las cuales establecÃan un planeta oculto en ese punto. Algo asà como el gemelo malvado de la Tierra jajaj.
Un poco de eso acá:
http://tvtropes.org/pmwiki/pmwiki.php/Main/Counter-Earth
Respecto a lo que pregunta Fede Riveiro: en realidad nunca se está quieto, sino que a más o menos la misma distancia de los cuerpos que forman el sistema.
..y viendo el panorama de forma global: si bien el espacio se presume infinito, no asà la cantidad de cuerpos celestes. Asà que deberÃa haber en toda la infinidad del espacio algunas zonas en donde realmente te quedás quieto (se puede decir "respecto al sistema" si estás abarcando TODO?)... aunque imagino que con los movimientos de los cuerpos esos puntos podrÃan cambiar radicalmente de un lugar a otro pasando de una quietud total a una turbulencia loca en un instante....
tal cual estimados, son puntos de "más o menos equilibrio" que no significa un equilibrio teórico perfecto, siempre necesitás estar corrigiendo todo, es simple, si pasa un asteroide más o menos cerca ("cerca" a escala espacial) ya te tironea para un lado y otro, es imposible no estar siendo sometido a alguna fuerza de atracción en el espacio y menos cuando estas dentro de un sistema solar bien activo.
Eso es en la practica, no? Ya que se desprecian valores muy bajos de otro tanto de fuerzas que actúan, ya que dos cuerpos para que no se atraigan tienen que estar a distancia infinita,
Profe, profe, no entendà profe.
L1 perfecto, pero los demás no logro comprenderlos. Tomando como referencia la imagen, los vectores de fuerzas en L4 y L5 se pueden anular en el eje X, pero en el Y van a apuntar hacia abajo y hacia arriba respectivamente cuando se sumen. Lo mismo con L2 y L3, la suma de los vectores de fuerza terminan apuntando hacia la izquierda y hacia la derecha respectivamente. Y si hay vectores de fuerza no nulos hay aceleración, si hay aceleración hay velocidad y si hay velocidad hay movimiento. A menos que sea que la fuerza es despreciable en esos puntos o áreas, pero en realidad seria a partir de ahÃ, ya que cuando más te alejas menos actúa la gravedad. Por lo menos hasta que entre en escenario un cuarto cuerpo, como Marte, a romperte las pelotas.
tal cual estimados, son puntos de "más o menos equilibrio" que no significa un equilibrio teórico perfecto, siempre necesitás estar corrigiendo todo, es simple, si pasa un asteroide más o menos cerca ("cerca" a escala espacial) ya te tironea para un lado y otro, es imposible no estar siendo sometido a alguna fuerza de atracción en el espacio y menos cuando estas dentro de un sistema solar bien activo.
12/11/2012 - 00:55:58
